The Partial Fraction Algorithm
The following theorem is the heart of the partial fraction method. Applied recursively to the denominator, it produces the partial fraction expansion of any rational function.
Theorem 3
Let 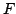 be a field, and let
be a field, and let 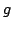 ,
, 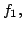
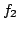 be polynomials in
be polynomials in
![$ F[X]$](img22.png) such that
such that 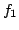 and
and 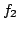 are coprime
and
are coprime
and
 . Then one may write
. Then one may write
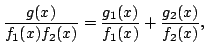
with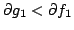 and
and
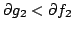 .
.
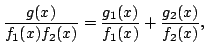
with
Indeed, as ![]() ,
, ![]() are coprime, we may apply Theorem
2 and deduce that there exist polynomials
are coprime, we may apply Theorem
2 and deduce that there exist polynomials ![]() ,
, ![]() such
that
such
that
Now let ![]() be an arbitrary polynomial (to be fixed later) and define
be an arbitrary polynomial (to be fixed later) and define
Then
Now given
and we take this for the definition of our polynomial
We now flesh out the algorithm by giving the full partial fraction expansion.
Corollary 1
Let 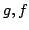 be polynomials such that
be polynomials such that
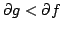 ; and
write
; and
write
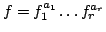 , where
, where
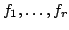 are
mutually pairwise coprime polynomials (that is, no pair of
polynomials has a non-trivial common factor), then one can express
are
mutually pairwise coprime polynomials (that is, no pair of
polynomials has a non-trivial common factor), then one can express
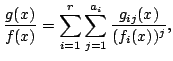
for some polynomials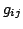 such that
such that
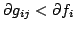 .
.
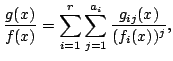
for some polynomials
Using our partial fraction algorithm (Theorem 3), a
simple induction gives
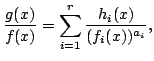
for some polynomial
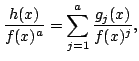
for some polynomials
This is trivial for ![]() , and for
, and for ![]() , we employ Euclid's algorithm
to give
, we employ Euclid's algorithm
to give
with
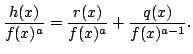
As in the proof of Theorem 3, one can show that
Finally, we can employ this result to recover the familiar high school partial fractions result for real polynomials.
Corollary 2
Let 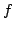 be a polynomial over
be a polynomial over
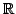 and let
and let 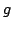 be a
polynomial over some extension field of
be a
polynomial over some extension field of
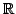 (e.g.
(e.g.
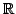 itself,
itself,
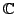 , etc.). Write
, etc.). Write
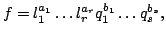
where the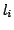 are linear polynomials and the
are linear polynomials and the 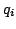 are
quadratic polynomials, all of which are mutually pairwise coprime.
Then there exist constants
are
quadratic polynomials, all of which are mutually pairwise coprime.
Then there exist constants
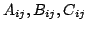 in the extension field such
that
in the extension field such
that
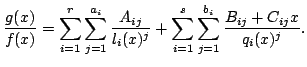
The proof is left to the reader!
where the
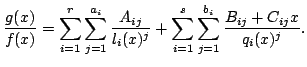
Gihan Marasingha 2005-09-19